
Viendo esta entretenida película lo que más me sorprendió, aunque no lo único, fue que los protagonistas se encontraran vida "ahí abajo". Para que exista esa vida el ecosistema precisa de una
fuente de energía externa, de una fuente de carbono, un donador de electrones y de otros elementos imprescindibles para la vida.
Las fuentes de energía pueden clasificarse en dos categorías amplias: los organismos que son capaces de obtener energía a partir de la luz, llamados fotosintéticos, y los que la obtienen a partir de reacciones químicas, los quimiosintéticos.
Las fuentes de carbono son también dos: el carbono orgánico, siendo los organismos heterótrofos, como los humanos, o autótrofos, en los que se usa el dióxido de carbono.
En cuanto a los donadores de electrones que usan hay organotrofos, que usan donadores orgánicos, y litótrofos como algunas bacterias, que los precisan inorgánicos.
Todos estos mecanismos se combinan en las diferentes especies, dando lugar a nombres más complejos como podéis ver en el enlace de arriba que dirige a la Wikipedia.
En la
película los únicos productores, aquellos organismos que transforman materia inorgánica en orgánica, parecen ser las plantas como se ve en el vídeo del enlace, que son fundamentalmente organismos fotosintéticos y autotrofos, es decir, necesitan luz y CO2. Vamos a suponer que en el interior de La Tierra hay luz, como se ve en la película.
El primer problema podría ser la presencia de dióxido de carbono en el subsuelo, pero si las erupciones volcánicas
liberan este gas podríamos pensar que no es un limitante, ya que los personajes entran y salen a través de volcanes. Menos incluso en un futuro si hay
proyectos que pretenden enterrarlo para evitar su exceso en la atmósfera, aunque este no es el caso de la película.
El mayor problema viene cuando observamos los factores físicos que limitan la fotosíntesis, como la
temperatura; en este gráfico se puede ver como la eficiencia aumenta hasta un valor máximo, a partir del cual decae:

Todas las reacciones químicas aumentan su velocidad con el ascenso de la temperatura, y la fotosíntesis no iba a ser menos, pero a partir de ciertos valores la eficiencia disminuye por rotura de las proteínas que intervienen en el proceso.
Por lo tanto, si los protagonistas hablan de temperaturas máximas de 93ºC no solo la fotosíntesis se hace inviable, sino también la vida de la planta.
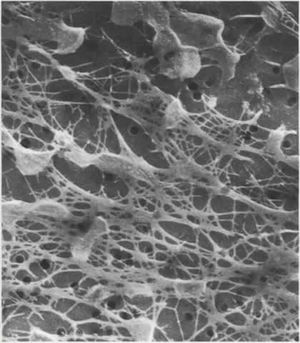
Si descartamos a las plantas nos quedaríamos con las bacterias, que las hay de todos los tipos mencionados al principio, y que además algunas pueden resistir condiciones ambientales extremas, es decir, son extremófilas (
Pyrodictium en la imágen viviría comodamente a los 93ºC). A esas profundidades nos podemos encontrar con los
SLiME (Subsurface Lithoautotrophic Microbial Ecosystem), ecosistemas de bacterias que usan fundamentalmente el hidrógeno molecular como donador de electrones, pero que crecen muy lentamente porque esta molécula es escasa en la corteza terrestre.
Por lo tanto, no se puede formar un ecosistema tal y como los de la superficie terrestre, con organismos macroscópicos, la física lo impide, la temperatura es excesiva y el entorno carece de las sustancias necesarias.
Fuentes, aparte de los enlaces:
Azcón-Bieto J.:
Fundamentos de Fisiología Vegetal 2008
Apuntes de clase.




